HELIKUTU KOBO

へりくつ工房はカードゲームを作ったり、 そうでもないものを作ったりしています

ヘクスマップにおける双対グラフへの変換と応用への一考察

2024年12月22日 投稿者: 天空　薙

この記事はなに？

この記事はBoard Game Design Advent Calendar 2024の22日目の記事として書かれました。

こんにちは。
初めましての方は初めまして、お久しぶりの方はお久しぶりです。
HLKT工房の天空 薙と申します。
以後お見知りおきを！
ここ数年12月22日に記事を書いていたはずなのに、今年はナチュラルに登録した日を23日だと思い込んでギリギリになってしまいました！ごめんなさい！！

アドベントカレンダー登録時には、「ゲームマーケット2024秋に無人販売所を作ってみた」という記事を書くつもりでしたが、このアドベントカレンダーの1日目、戸塚中央さんの「 ヘクスマップのインタラクションについて」を読んで本記事の内容を思いついたので記事の方針を切り替えました。
突貫で作成した記事ですので、粗もありますが変なこと考えるやつがいるなぁくらいで見てやってください。

ヘクスマップの双対グラフへの「ズラし」

先程紹介した戸塚中央さんの記事では、ヘクスマップの図形的な要素（面、辺、点）及び、それらの一時的な占有（共有）、永続的な占有（共有）という切り口でプレイヤー間のゲームを分類でき、それらの要素に対して、「ズラし」をすることで別のゲームとして形になるのではないか？という発想で書かれています。
この「ズラし」の1形態を考える際に、せっかく六角形を充填された図形を用いるので、幾何学的な知見が使えないかと考え、図形の「面と点」を入れ替えた図形「双対グラフ」を考察してみると面白いのではないかと考えました。
小さいヘクスマップを考え、その双対グラフ（正三角形を充填したマップ）上でカタンのルールを置換してみました。

双対グラフについて

今回の話の中心になる双対グラフに関して紹介します。
定義としては

グラフ理論において平面グラフGの双対グラフ（そうついグラフ、英: Dual graph）とはすべての頂点がGの各面に対応するグラフである。Gの双対はGの面どうしをつなぐ辺があるとき、それに対応する辺を持ち、辺の両側が同一面である場合、自己ループ（英語版）する。Gの各辺eは対応する双対辺をもち、この辺はGの面に対応する双対頂点どうしをつなぐ。双対は平面グラフ（すでに平面への埋めこまれているグラフ）についての性質である。

Wikipediaより引用

と、小難しいことが書かれておりますが、誤解を恐れずざっくりと説明すると
「面を点に点を面に入れ替えた図形」を双対グラフと言います。
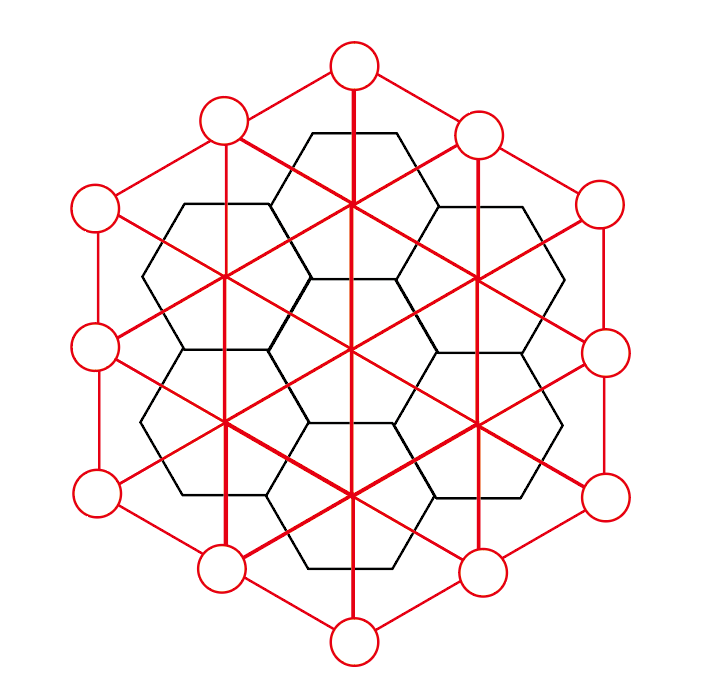
言葉だとわかりにくいと思うので、小さいヘクスマップで図示してみるとこのようなものになります。

黒い線が元々のヘクスマップ
赤いものが双対グラフのようなものとなります。
なぜ、”のようなもの”とついているかというと、黒い線の外側は1つの面として考えられるため、
下記の図の〇部分は1つの点としてくっついていなければなりません…（がヘクスマップを考える際にその外側も六角形が広がっていると考え、見やすさも考慮して今回はこの図を使っていきます。

双対カタンを考えてみる

小さいヘクスマップとそれの双対グラフを作成したので、この小さいヘクスマップ上でカタンっぽいものを考えてみます。
カタンは多くのルールがありますが、単純化のため下記のルールだけ抜き出します。
（道のルールとかまで入れると話がややこしくなるので、とりあえず以下の3つだけ）

  1. 面には資源と数字が割り振られている
  2. 点上にはプレイヤーは開拓地コマを置くことができる
  3. 同じ辺を共有する形で開拓地コマを置くことはできない

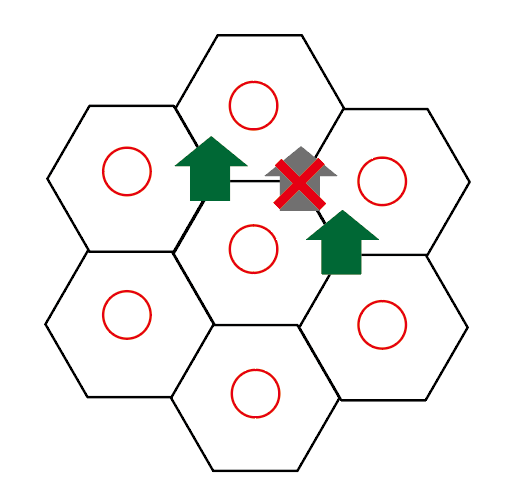
この状態をミニミニカタンと呼びます。
ざっくりと図示すると下記のような形になります。（ルール１に関しては図の簡略化のため、〇で表しています）

このミニミニカタンを双対グラフ上へ移動させます。
双対グラフでは面→点、点→面と変換するため、ルールとしては下記のようになります。

  1. 点には資源と数字が割り振られている
  2. 面にはプレイヤーは開拓地コマを置くことができる
  3. 同じ辺を共有する形で開拓地コマを置くことはできない

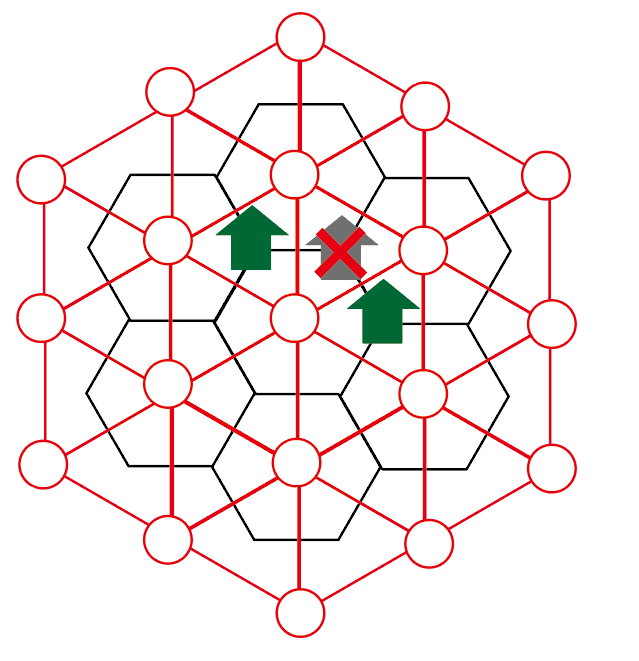
これを先ほどの図に重ねてみますとこのようになります。

そして、コマをタイルにして、ミニミニカタンの要素を消すと…

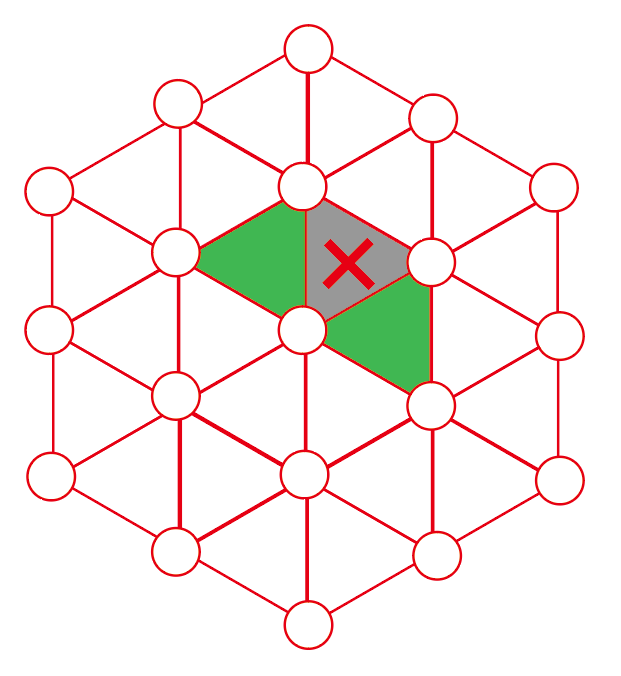
といった感じで、元々カタンだったとはぱっと見わからない形になっているかと思います。
また、ルールの「3.同じ辺を共有する形で開拓地コマを置くことはできない」に関しては、双対カタン上では、「タイルに隣接する形でタイルを置くことはできない」と読み替えることができます。

まとめ

ということで、ミニミニカタンに対する双対概念である、双対カタンがあるとしたらどういった形になるかを考えてみました。
このままではすぐ何かに使える！というアイデアではないですが、ちょっと面白いことができそうだなということで、作成してみました。
こんな感じのズラしもおもしろいんじゃない？という天空からの提案となりました。
ヘクスマップでお悩みの方！三角形の敷き詰めマップ（名前を知らない）なんてどうでしょう！（笑

最後に

最後になってしまいましたが、今回の記事の着想となった戸塚中央さんへ感謝を述べさせてください。
あと、次回作楽しみにしてます！（私信）

あ、ちなみにスクエアマップの双対グラフはスクエアマップになります

明日のBoard Game Design Advent Calendar 2024はUkiUkiさんの「好きじゃなかったトリテを今年２作品作ったことについて」です！
お楽しみに！！